병합 정렬이란?
- 병합 정렬의 경우에는 분할 정복 알고리즘을 사용하고 있다.
- 분할 정복은 더 이상 쪼갤 수없는 크기가 될 때까지 분할해야하기 때문에 재귀함수로 구현해야한다.
- 단점: 재귀함수를 사용하게 되면 함수 호출이 많이 발생되며, 오버헤드가 발생한다. 즉, 메모리를 많이 사용하게 된다.
- 장점: 시간 복잡도 O(NlogN)을 보장하는 빠른 정렬 알고리즘이다.
분할 정복이란?
1. 분할(divide): 큰 문제를 작은 부분 문제(쉬운 문제)로 분할한다.
2. 정복(conquer): 작은 부분 문제를 각각 해결한다.
3. 조합(combine): 해결한 부분 문제의 답을 이용하여 다시 큰 문제를 해결한다.
병합 정렬 동작 방식
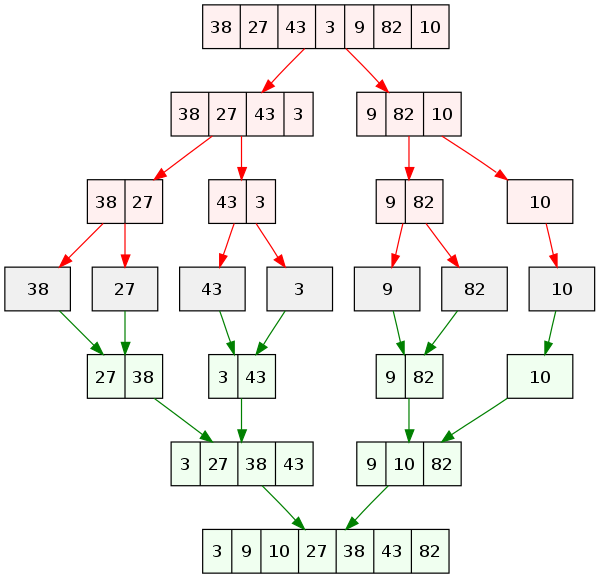
=> 각 부분 배열은 이미 정렬된 상태로 보며, 각 부분 배열의 첫번째 원소부터 시작하여 하나씩 확인한다. 그리고 비교 후 작은 값을 임의의 배열에 저장한다.
const mergeSort = (arr, left, right) => {
if (left < right) {
//중간 값을 기준으로 sort하기 위해서 mid를 구한다.
let mid = parseInt((left + right) / 2);
//이젠 중간값을 기준으로 값을 나누기 위해 왼쪽부터 sort한다.
mergeSort(arr, left, mid);
//오른쪽 을 sort한다.
mergeSort(arr, mid + 1, right);
//이젠 sort하고 병합하는 함수를 불러온다.
merge(arr, left, mid, right);
}
};
const merge = (arr, left, mid, right) => {
let leftNumber = left;
let rightNumber = mid + 1;
//sort된 값을 저장하기 위해서 임의의 배열을 만든다.
let sortedArray = [];
let sortedKey = left;
//왼쪽의 첫번째자리수가 중간값과 같아지거나, 오른쪽의 첫번째 자릿 수가 끝 수랑 같아진다면 반복문은 끝난다.
while (leftNumber <= mid && rightNumber <= right) {
//배열에서 왼쪽의 첫번째 자리보다 오른쪽의 첫번째 자리가 크다면 왼쪽의 첫번째 자리의 수를 저장한다. 아니면 반대로 저장되다.
if (arr[leftNumber] <= arr[rightNumber])
sortedArray[sortedKey++] = arr[leftNumber++];
else sortedArray[sortedKey++] = arr[rightNumber++];
}
//위에서 leftNumber++를 했기 때문에 기존 자릿 수 보다 더 많아짐. 즉, 왼쪽 배열이 없는 상태.
if (leftNumber > mid) {
//나머지 오른쪽 배열을 임의의 배열에 저장한다.
for (; rightNumber <= right; rightNumber++)
sortedArray[sortedKey++] = arr[rightNumber];
//위에서 rightNumber++를 했기 때문에 기존 자릿 수 보다 더 많아짐. 즉, 오른쪽 배열이 없는 상태.
} else {
//나머지 왼쪽 배열을 임의의 배열에 저장한다.
for (; leftNumber <= mid; leftNumber++)
sortedArray[sortedKey++] = arr[leftNumber];
}
// 임의의 배열을 기존 arr에 저장한다.
for (let x = left; x <= right; x++) {
arr[x] = sortedArray[x];
}
};
let arr = [3, 5, 2, 8, 1, 9];
mergeSort(arr, 0, arr.length - 1);
console.log(arr);
참고
패스트캠퍼스 알고리즘 강의를 들으면서 정리,
'알고리즘' 카테고리의 다른 글
| [JS 알고리즘] 특정 범위에 해당하는 원소 개수 구하기(lowerBound,upperBound) (1) | 2023.12.27 |
|---|---|
| [JS 알고리즘] 순차 탐색과 이진 탐색 (1) | 2023.12.26 |
| [JS 알고리즘] 백준 17609 (0) | 2023.12.07 |
| [js 알고리즘] 백준 9009: 피보나치 (0) | 2023.11.28 |
| [JS알고리즘] 선택 정렬, 버블 정렬, 삽입 정렬 (2) | 2023.11.22 |
